7+ Taskbar Tweaker
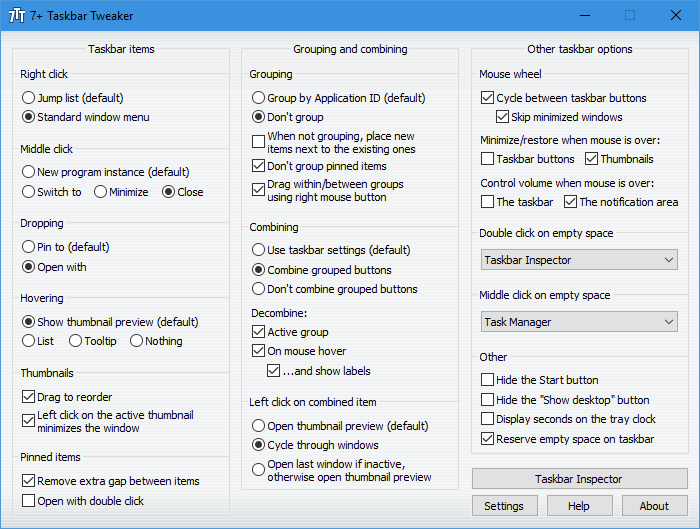
7+ Taskbar Tweaker allows you to configure various aspects of the Windows taskbar.
Most of the configuration options it provides can’t be tweaked using the taskbar properties or the registry.
The tweaker is designed for Windows 7, Windows 8, and Windows 10.
Download
![]() 7tt_setup.exe (1.78 MB, changelog)
7tt_setup.exe (1.78 MB, changelog)
Latest version: v5.15.1
Note: The installer can be used to extract a portable version. Refer to the FAQ below for details.
Beta version
![]() 7tt_setup_beta.exe (1.79 MB, changelog)
7tt_setup_beta.exe (1.79 MB, changelog)
Latest beta version: v5.15.1.2
More info about beta versions.
✖
Windows 11 Support Status
- 7+ Taskbar Tweaker doesn’t support the Windows 11 taskbar, and probably never will. See this blog post for more details.
- Some of the tweaks are available in Windows 11 as Windhawk mods. See here for the list of mods, and vote for missing mods that you’d like to see implemented. Read more about Windhawk here.
- 7+ Taskbar Tweaker works on Windows 11 with the old taskbar which can be restored with third party tools. See this blog post for more details.
Demo video
Here is a video that demonstrates some of the tweaks:
Source code
https://github.com/m417z/7-Taskbar-Tweaker
FAQ
Q: Which registry keys does 7+ Taskbar Tweaker modify? I don’t need extra processes in my system.
A: The only registry keys the tweaker modifies are its own settings. There are no registry keys for the options it provides. The tweaker does that by injecting a DLL to explorer, hooking/subclassing/some other methods of the dark side.
As for extra processes, the tweaker is a native program, and is very lightweight. It shouldn’t slow down your system, and uses an extremely small amount of memory. Also, you can hide the tray icon if you want.
In case you want to remove the tweaker’s settings from the registry, look for them here:
HKEY_CURRENT_USER\Software\7 Taskbar Tweaker
HKEY_CURRENT_USER\Software\Microsoft\Windows\CurrentVersion\Run (“7 Taskbar Tweaker” value)
P.S. if you’re a programmer, you might want to take a look at the 7+ Taskbar Tweaking Library.
Q: My antivirus complains about 7+ Taskbar Tweaker.
A: It’s a false positive. I guarantee that the tweaker binaries (and any other files on this site, unless specifically noted) are 100% clean.
Also remember that the tweaker injects into explorer and modifies its memory, which is indeed suspicious.
Q: Can I Group/Combine/Label only some of the items on the taskbar?
A: Yes, use Taskbar Inspector.
Q: May I use 7+ Taskbar Tweaker in a commercial environment?
A: Yes, feel free to use it wherever you want.
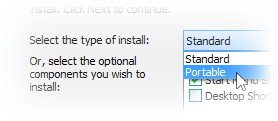
Q: Where is the portable version?
A: When installing the tweaker, choose the Portable type of install, as shown on the image below.
The portable version will be extracted to the selected folder.
Note: If the tweaker is already installed on your computer, the option won’t be visible. You can launch the setup with the /portable command line switch to force a portable installation.
Q: I want to report a bug/suggest a feature! What is the best way to do it?
A: Post it on the UserEcho page.
Q: I want to translate 7+ Taskbar Tweaker to my language.
A: The archive below contains the files needed to be translated.
Please read readme.txt before proceeding.
![]() 7tt_translate.zip (758.63 kB)
7tt_translate.zip (758.63 kB)
If you are brave enough to translate the help file, contact me for the required software and files.
Tags: 7+ taskbar tweaker
Not sure what happened, but 5.9.0.10 doesn’t work here. Immediately fails with the usual message when I install it. Reverting back to 5.9 release and keeping Windows updates entirely disabled. I’ve lived without them for the last year, I don’t need Windows updates for another year.
Windows 10 2004 x64 without KB4566782.
I believe that 5.9.0.10 had an issue with a specific explorer build, please try 5.9.0.11.
I have noticed some unexpected behavior when using virtual desktops in windows 10. When using 2 virtual desktops the sorted taskbar items reverse to where they where when you switch from one virtual desktop to the other. This basically makes this program useless when using virtual desktops. I am using windows 10 pro, version 1909, build 183631016. Maybe I am missing something and doing something wrong, if so, please enlighten me. Thanks 😉
By default, the order of the taskbar items is not preserved. You can use the
virtual_desktop_order_fixadvanced option to solve this. See here.Hello. Rammichael ty for ur awesome tool. I needed to ask about 1 think, can u add to ur tool checkbox about hiding this(https://pastenow.ru/AFEL1) button & change the “show desktop” function to the tray button. Again thanks
Hi,
That’s not a popular request, so I’m not sure it will ever be implemented in the tweaker, but maybe one day.
What do you mean by that?
its 1 request not 2, hide it(https://pastenow.ru/AFEL1) and give it functionality(expand to see system tray icons) of this button(https://pastenow.ru/AFEL1) to ShowDesktop button.
I understand. Still, it’s a very specific and uncommon feature request (for a kiosk mode or similar?), so as I said, maybe one day but don’t hold your breath.
thanks anyway, ur tool is awesome.
OS:
Windows 10 Pro 64bit v1909
7tt:
v5.9.1
Combine not working for left/right vertical taskbar positions – works just fine for bottom/top horizontal positions.
I mean interactive single program group combine, like:
“Taskbar Inspector->right click program executable->Combine Always->Always->on”
nothing happens, if position bottom/top works just fine.
And 7tt v5.9.1 works OK for all positions on Windows 7.
Thank you for reporting. I was able to reproduce the problem, and will investigate it when I have some spare time.
I looked at it, and here’s some information:
The combining functionality is implemented differently in Windows 7 and in Windows 10, and in both cases the implementation is quite tricky and fragile.
In Windows 10, due to the way it’s implemented, it only works on a horizontal taskbar. It took only five years for somebody to notice 🙂 so looks like it’s not a commonly requested feature.
I tried to find a simple solution, but couldn’t come up with something. Perhaps I’ll revisit it one day in the future.
Luckily for you, there’s a workaround. Set the taskbar to “Always combine, hide labels” in system taskbar properties. Then set the “show_labels” advanced option of the tweaker to “2”. Finally, select “Don’t combine grouped buttons” if that’s the default configuration you prefer.
Hi RaMMicHaeL, first off let me tell you that I think you are an awesome dev and wanna thank you for making 7+TT, it’s just so well made and super useful.
The new Windows 10 October 2020 final build has been released and I’ve been wanting to upgrade. I read that this update is small and mostly just activates dormant features from the current build. Will 7+TT (v5.9.1) still work if I upgrade? Is a beta currently in the works that support it?
Thank you.
Hi,
I didn’t try it and I’m not sure whether it’s supported. If it indeed only activates dormant features, then I believe that it should just work. If you get the chance to try it out, feel free to post your findings 🙂
It works!
First off, like everyone else here, I absolutely LOVE this program. It is in use every single day.
I just upgraded Win10 Oct and now it does not work.
I get the error: Could not load Library (5)
Win 10 Home
10.0.19041 Build 19041
And the funny part of all this is for as long as I have been using this program to reorder my programs (like when you have 15 excel files on the go lol!), I have just found a lot more things to do with it now by searching the site to see if anyone else is having issues since the Oct update. So blessing in disguise?
Thank you for all the work you’ve put into this.
Hi,
I’m glad that you’re enjoying the tweaker. Blessing in disguise for sure 🙂 I hope that you also found out that you can use the beta version for now to solve the library loading error.
Bonjour,
Problème avec le logiciel, il nous dit qu’il n’arrive pas a charger la bibliothéque ???
Thanks, solved my problem
Will the program be getting renamed to 10+ Tweaker seeing as MS no longer supporting Win7?
No, 7+ Taskbar Tweaker will continue to support Windows 7, even thought Microsoft doesn’t anymore.
Just want to say thanks for everything you do. I’m sure it’s not easy but it is very much appreciated.
For reference, I’m running Windows 10 Enterprise x64. It’s most impressive that you were able to get Windows, your arch nemesis, to notify me of an update with its built-in notifications backend. The changelog was to the point and had all of the key information one would need (date of update, changes, revision etc).
The process of updating third-party software usually goes like this:
User not notified until they open the program (i.e they have a current task and are likely not expecting to spend the next 2 minutes updating software). User is prompted “An update is available for ___, do you want to download it?” (tells you nothing more at this time)
User has to decide between putting off what they were doing to update the program or delaying the update (not a big deal but it’s not intuitive from a user perspective). Let’s say they click yes to update.
Web browser opens to a page
User has to locate the correct download button for their OS and architecture (sometimes browsing multiple pages)
User clicks download
User clicks browser pop-up to confirm the download
User waits for download, then clicks the browser downloads button
User clicks the setup .exe from the drop-down list
User clicks to confirm running of unsigned setup .exe
User waits for install wizard to open
User clicks next on wizard page 1
User clicks next on download location
User clicks install on changes page (if they are shown at all that is..)
User clicks finish
User has to re-open program manually and check version
Updating your 7+ Taskbar Tweaker:
Accepted the update from tray icon (2 clicks total, I believe)
Program displays a progress bar
Program restarts and is now up to date
All in all, it took like 4 seconds for this whole process. Fantastic job, thank you thank you thank you!
Thanks for the great feedback! The goal was to make the update as seamless as possible, yet informative. I’m glad that the work is appreciated.
7+ v5.9 doesn’t work after Windows 10 did an update just now. When starting it says “7+ taskbar tweaker could not load library (5)”.
Exact same problem for me. Remove 7TT and install the beta (currently v5.9.0.11) instead.
I have same message than others after last updtate to windows 10 v 2004:
When starting it says “7+ taskbar tweaker could not load library (5)”.
I didn´t want update windows 10 but it was necesary!!
The incompatibility problems should be fixed in 7+ Taskbar Tweaker v5.9.1.
Thank you!
At the moment I´ve tried with Beta version and it works
How do I download the beta version. Link on download page isn’t working. Thank you! I love this product but it suddenly stopped working.
The link works for me. You can try using this alternative link. Perhaps the download link is blocked by your security software because of a false positive detection, in which case this link might not work as well.
A lot of antivirus software mark this tool as a virus (false positive, for obvious reasons). May I suggest signing the executable? This will give antivirus software information about the legitimacy and origin and will reduce the false positives.
Thanks for the feedback. I’d do that if that was simple. Unfortunately, the process is not hassle-free (and the signature itself is not free).
Here are the insights of the Notepad++ developer on the matter:
https://community.notepad-plus-plus.org/topic/17184/remove-code-signing-from-notepad
On the upside, the “false positive period” is usually relevant only when a new version is released. After a week or two, the tweaker is added to the white list of antivirus vendors and it ceases to be a problem, until next update.
That makes sense. Thank you for your reply and the great tool! I can’t work without it, so luckily my IT department whitelists the executable for me. 😉
As I alredy replied, Virustotal does NOT detect anything on both 7+ Taskbar Tweaker.exe and inject.dll.
HOWEVER, the installer 7tt_setup.exe is detected by 6 engines!!
https://www.virustotal.com/gui/file/0f1a062fcff547c3068caeb2c87a19b5c3165b33b58805c7cc707327cc987c45/detection
AegisLab -> Trojan.Win32.Generic.4!c
SecureAge APEX -> Malicious
Avira (no cloud) -> TR/Crypt.XPACK.Gen
F-Secure -> Trojan.TR/Crypt.XPACK.Gen
Ikarus -> Win32.Outbreak
McAfee -> Artemis!FE1DA0A82443
Which installer tool or libraries are you using?
It’s NSIS with the following included:
Feel free to extract and analyze all files. Also feel free to report about it to the relevant AV companies to make sure that this is a false positive.
Thanks for your reply. Yes, apparently NSIS installer is often detected as containing viruses, take a look at that:
https://nsis.sourceforge.io/NSIS_False_Positives
Cheers,
Interestingly enough, Virustotal does NOT detect anything on both 7+ Taskbar Tweaker.exe and inject.dll.
HOWEVER, the installer 7tt_setup.exe is detected by 6 engines!!
https://www.virustotal.com/gui/file/0f1a062fcff547c3068caeb2c87a19b5c3165b33b58805c7cc707327cc987c45/detection
That’s kind of concerning…
I am unable to download v5.9.1 of 7tt_setup.exe and keep getting an error message saying something along the lines of “This file in not commonly downloaded”.
You see this message because the new version was just released and is still not popular enough. You can either choose to open it anyway (Click on “Open”, then “More info” -> “Run anyway”). Alternatively, download it in a couple of days, hopefully the message won’t be shown anymore by then.
Latest version 5.9.1 working great. Don’t worry about the warning just false positive being new version.
Thank you for the new updates and all your hard work! I just wanted to say I love how easy/seamless it is to update your program, and how simple it is to switch between stable/beta branches. Much appreciated as always!
Had BETA 5.9.0.9 installed fine after latest Win10 update, got notice today of new version 5.9.1. McAfee now warns me of the download website for the first time. Turned McAfee off to download, then back on, and now it will not let me install the program as it states virus “Suspect!fe1da0a82443” is in the setup file “7tt_setup.exe”. I’ve tried several times, same result.
Anyone experiencing this? Michael is an honest guy, so I’m sure this is some anomaly.
Michael, you can cancel the note I just left a few mins. ago, I now see the few previous posts about this issue being false positive bc it’s new.
Is the rumored Portable version not yet ready?
Just select the portable installation 🙂 see the answer in the FAQ above about choosing the portable installation type.
Dude, are you fcuking kidding me?? Thank you so much for such tool!!!!!!
So simple and so useful!
🙂
Thank you so so much for the new update! Love the HiDPI support!
Thank you for the high dpi mode it makes the window look so much better
You still haven’t updated at all. V5.9.1 still doesn’t work with the latest Windows 2004 update. Only the beta works with it.
v5.9.1 and v5.9.1.1 should behave the same way on Windows 10 version 2004, unless you’re using an insider build.
I’ve never been an insider at all. But it doesn’t work with the latest Windows update. I do check for updates everyday though.
Are you sure that you were running v5.9.1? What error message were you getting with it? What’s the version of the explorer.exe file on your computer?
It works now. I just downloaded it again and it works. So now I have no error to give.
Great. Perhaps you were running v5.9 and not v5.9.1. If you see an error again please let me know, thanks.
CAREFUL, I updated via app and I got a bitcoinminer malware.
Trojan.BitCoinMiner, C:\WINDOWS\SYSTEM32\WINRMSRV.EXE, En cuarentena, 925, 767022, , , , , 462EE20E8ABBBB559BD1C4F8BE87B123, 5B85CEB558BAADED794E4DB8B8279E2AC42405896B143A63F8A334E6C6BBA3FBTrojan.BitCoinMiner, C:\WINDOWS\SYSTEM32\WINLOGUI.EXE, En cuarentena, 925, 767023, , , , , FB9F4EB58354E9D3D6B7F84F5D12B639, 91BFB82ED5C32979368EDDCD34861B631926D2352D16ADF189944C4BA8CCF4E1
Backdoor.Agent, C:\WINDOWS\SYSTEM32\TASKS\Microsoft\Windows\WDI\SrvHost, En cuarentena, 865, 653659, , , , , 75503BD9F157A844491ECCCEAF75CEB1, 7786939A04F386D1C354FF8FDE29A4570D4A95AFB3118DD6017D3A1421B237F6Backdoor.Agent, C:\WINDOWS\SYSTEM32\WINSCOMRSSRV.DLL, En cuarentena, 865, 653659, 1.0.29193, , ame, , 919611928882E781ABAB300BF9227374, CBDD93BA08E87007665250C3253A1FE9AD38511E4A8A2E5305ADC0F36E43AB44
How did you come to the conclusion that it’s related to 7+ Taskbar Tweaker?
any way to get again the version v5.9.0 ?
thanks
You can get it, and other previous versions, here. May I wonder why you need it? What’s wrong with v5.9.1?
Today I restarted my laptop and AVG prompted me to restart to remove 7+ Taskbar Tweaker as “this is the only way to contain the threat”. Also, on VirusTotal the latest 7tt_setup_beta.exe has 6/70 hits [1] and the latest 7tt_setup.exe has 2/70 hits [2].
[1] https://www.virustotal.com/gui/file/530b173c686d83542391927c4f0880910fd822bf8e90fdeea0b42d6527451066/detection
[2] https://www.virustotal.com/gui/file/0f1a062fcff547c3068caeb2c87a19b5c3165b33b58805c7cc707327cc987c45/detection
While I suspect these are false positives, it makes me feel a bit too uneasy to keep 7+ Taskbar Tweaker installed on my laptop.
Those are false positive detections. False positives are unfortunately common for new versions of 7+ Taskbar Tweaker and for beta versions which are less common. Please see the FAQ here and this blog post.
Also, Matthew, please understand that I have no control over the antivirus companies. While it makes me sad to read about your thoughts of stopping using the tweaker, I’m afraid that there’s not much that I can do about it. Perhaps the fact that the tweaker exists for more than a decade (!), with many false positive detections but no actual incidents, can help convince you to keep using it.
Hello. Is there a support page that displays the hash for the download to verify? Or is that a non-trivial request?
Hi Sean,
There’s no such page, and frankly, I don’t see much value in it. If you want to make sure that the file is not corrupted, the setup program already has an integrity verification, just run it. If you want to make sure that the file wasn’t replaced with a malware, such page won’t be too helpful:
https://security.stackexchange.com/questions/1687/does-hashing-a-file-from-an-unsigned-website-give-a-false-sense-of-security
You can upload the file to VirusTotal. In addition to the scan results, I try to leave a comment on each version that was compiled on my computer.
Yes, I just started to read up more on it and value is marginal. Thanks for your time.
I got “Error opening file for writing” with v5.9.0.11 on Windows 10, version 2004.
,but I was able to run and use in portable mode though
What’s the exact error message? Is it “Error occurred while saving configuration”?
This is odd, it was my anti virus, but I was not getting the same error as everyone else(using AVG), It installed fine and worked on the current beta for a week, then it stopped working, but I have not added it to an exception list. Sorry for your time. Love the program so much.
Look like last cumulativ update (2004) completely removed 7TT (today)
I haven’t experienced the problem when I updated my own computer to the latest update. Do you have a third party antivirus installed? Perhaps it removed the tweaker due to a false positive detection.
Hi, i have windows 10 (2004) and i have a problem, when i try to delete a file on the desktop, i cant, and im receiving the error that says: you need permissions to do this action, i figured out that the error disapear if i close the 7tt program and restart the explorer. Some other times my antivirus (Avast) block an action that says > “7+ Taskbar Tweaker.exe” is trying to delete the file …., so i dont understand what is happening, this isnt happening before, someone with this problem too?
Michael, just an FYI that I’m getting the 107 error when running 7+ TT v5.9.1.1 Beta after I just upgraded to the following Windows Home Insider Preview build:
Windows 10 Home Insider Preview
Version 2004
OS Build 20211.1000
Just thought I’d let you know in case you haven’t heard yet. Looking forward to the 7+ TT beta that works with this OS Build.
Hope you’re doing well and thanks as always for your hard work.
Please try the newly released beta version, v5.9.1.2.
Beauty! Works like a dream! Thank you sir!
v5.9.1.1 (beta) not work on
Evaluation copy Build 20211.re_prerelease.200904-1619
Please try the newly released beta version, v5.9.1.2.
Hey there, first I wanted to say, thanks for this masterpiece! It eases my daily life. I donated some bucks to your wallet.
Recently I noticed my taskbar right-click context menu not working anymore. It will only show the basic items like Unpin and Close. Anything custom that the software itself might add is not seen anymore. First I thought its some Windows bug and I deleted several cache items. Nothing worked, except when I exited 7+ TBT.
The only thing I have done recently is to upgrade to 2004 and also update my 7+ Taskbar Tweaker. I don’t know which one is to blame. I also tried the latest beta but to no avail.
My settings: https://i.imgur.com/MlBsKVK.png
Example of correct context menu: https://i.imgur.com/wdxQ4OL.png
Cheers
Hi Jenga,
That might happen if you change an item’s AppId. Perhaps you did that with the right mouse dragging option (“Drag within/between groups using right mouse button”).
Open Taskbar Inspector and see whether the “restore” option fixes the issue: https://i.imgur.com/T9Frbt1.png
P.S. If that was the actual issue, I wouldn’t expect exiting the tweaker to fix it. Also closing and re-launching Firefox should solve it. Try out these things and let me know what you found.
Thanks for your reply. This actually happens to all my taskbar items. When closing 7+ TBT the context menu behaves normally again.
This issue persisted through multiple reboots already and is ongoing for about a week or so. Nonetheless I tried to restore the Appid, which did not seem to do anything (probably because it wasn’t changed).
Do you have an overview of old 7+ TBT versions? I might go back 2-3 versions and maybe it works again.
It’s a different issue then. Do you experience it if you restore all of the tweaker’s options to default? If not, could you track the option that causes this behavior?
You can find previous versions here, but they won’t work with Windows 10 version 2004.
I can confirm that deleting HKEY_CURRENT_USER\SOFTWARE\7 Taskbar Tweaker and starting 7+ TBT still causes this, with default settings then.
I don’t have ideas and I can’t reproduce it on my computer, but please provide me the following and perhaps I’ll have some insights:
10.0.19041.423
Version 2004 (OS Build 19041.450)
StartIsBack
All three versions you provided work 😀
That’s it, I could reproduce the problem with StartIsBack installed. I’ll see if there’s a possibility for a workaround on my side.
It looks like the issue occurs as long as 7+ Taskbar Tweaker hooks the
DPA_Createsystem function, even if nothing is done in the hook.Here’s a workaround version with the hook removed. The removed functionality: Taskbar Inspector is no longer updated in real time.
The implementation wasn’t changed for years in the tweaker, so it must be some change on StartIsBack’s side. I suggest contacting them to implement a fix. I won’t be maintaining this workaround tweaker version, which is only for a temporary fix until they solve it properly.
Also, looks like turning off the StartIsBack option fixes the problem.
Thanks a lot for checking this out! And helping me so fast. I’ve already contacted the developer and hope to get a compatibility fix. In the meanwhile, I’ll disable this option.
no_width_limit issue: I usually put the taskbar on the right and makes it narrowest. If I lock down the computer for a while (probably turn into sleep mode), the width will become wide again and I have adjust it again.
version: 5.9.1
windows 10 2004
os: 19041.508
Do you have external monitors attached to the computer? I’m asking to see whether the issue is similar to the one reported here.
No, I don’t have external monitors. This problem occured after I update my windows to 2004(not 100% certain if anything else was involved). I tested it again just now by changing my sleeping mode time setting to never, and it still become wide so sleeping mode is problably not the problem as well.
So it just returns back to being wide while the computer is running? Please try to come up with a way to reproduce the behavior so I can check it on my computer.
For my case, lock and close the screen and after a meal time unlock it the taskbar will be wide again.
I’ll try to look at it when I have some spare time. If you’ll be able to come up with more straightforward reproduction steps, it will certainly help.
Another finding may be useful. I use surface pro, when I try to remove the keyboard, the taskbar will become wide immediately.
That’s interesting, but unfortunately I don’t have a Surface to try it. If you’re able to reproduce it by other means, let me know.
This application is brilliant. This was an awesome find!
Hi Michael,
First off, big fan of 7TT for quite many years now!
I’ve migrated to a Windows 10 on an Arm device recently and I cannot get 7TT to work.
While the installer runs correctly, I’m guessing the executable is x64 as I get an error at launch about Windows not being able to execute the app; emulation for x64 is not currently supported.
I guess asking for a native Arm build is too much at this point 😉 but is there an option to get an x86/32-bit build of 7TT?
Thanks
Hi,
Arm versions of Windows aren’t supported. There are two variants of the tweaker, 32-bit and 64-bit, and the installer chooses the correct variant based on the OS. It looks like for an Arm OS it chooses the 64-bit variant. But even if it would choose the 32-bit variant, it wouldn’t work since explorer is a native Arm program.
If I ever get my hand on an Arm device, I might look into porting it properly.
Thanks, appreciate it, I’ll stay tuned in case you get a chance in the future 🙂
Hi, it looks like the userecho site isn’t working properly? I can’t click into any of the topics to view the details. Is it just me?
I’m having an issue with un-grouped UWP apps only showing their icon in the first instance of the program. If I open more they don’t have any taskbar icon. Is this a known problem?
Thanks
Works for me. Perhaps a temporary problem, please try again.
Regarding the UWP problem, I’m not familiar with it. Works fine on my computer, e.g. with Calculator. How can I reproduce the problem you’re seeing?
Here’s a clip showing my settings at the same time.
https://imgur.com/a/59zYAYX
You can see opening another instance of calculator puts the empty taskbar icon to the right. This only happens with UWP apps.
It’s using v5.9.1 on Windows 10 1909. This isn’t a recent change btw, I’m pretty sure it’s been like this for ages.
Ah, so there’s an icon, it’s just blank. This issue was reported before, but I thought it happens only for Edge:
https://tweaker.userecho.com/topics/336-multiple-instances-of-edge-dont-have-an-icon-when-grouping-is-disabled
I’ll take a look at it when I have time.
I also see from your clip that the “When not grouping, place new items next to the existing ones” option doesn’t work for UWP apps. Unfortunately there’s no easy fix for that. The notification that is sent for non-UWP apps (which was all there is back in the Windows 7 days) is not sent when a UWP app is launched. I might investigate it one day in the future. Meanwhile, I created a post about it on UserEcho.
Please try the newly released v5.9.1.3 beta. I believe that the issue is now fixed, as well as this long standing issue.
The beta works perfectly! Thanks so much! (Also the userecho site works for me now)
Hi Michael,
Thanks for the very useful tools.
I appreciate your will to share it with us. 🙂
However, do you know why my taskbar is always change to its ‘normal’ form after I exit from a game? It never able to keep its “tweaked” form everytime I exit from a game, so I need to change manually tweak it back after I finished the game.
I use a dell XPS 15 with 4k screen, and most of my game is on 1080 resultion. I think this resolution difference is the cause of the issue.
Is there any setting that I can use to fix this?
If there is any setting that I can use to solve this problem please let me know.
Thanks mate 🙂
Hi Siddhi,
Are you talking about a specific tweak? I’d assume that, for example, the no_width_limit option can reset itself if the system resolution changes, not sure. The other tweaks, at least most of them, shouldn’t be affected from launching a game.
Please provide more details about the things you need to tweak every time.
Greetings Michael!!
Just an FYI that I’m running 7+ TT v5.9.1.3 Beta and getting the following error at startup:
“7+ Taskbar Tweaker: Could not load library (5)”
I just upgraded to the following Windows Home Insider Preview build:
Windows 10 Home Insider Preview
Version 2004
Installed Oct 1, 2020
OS Build 20226.1000
Just thought I’d let you know in case you haven’t heard yet. Looking forward to the 7+ TT beta that works with this OS Build. Hope you’re doing well and thanks as always for your hard work!!
Have a great weekend my good sir!
Greetings!
Thanks for the info, I wasn’t aware of that. Please try the new beta version, 5.9.1.4.
Nicely done Mr. Michael! Problem solved, as always.
We should start calling you the The Librarian because Library Errors #107 and #5 don’t stand a chance against you!
Enjoy the rest of your weekend and thanks so much for the super-fast turn-around.
Hehe, maybe The Chaser since I’m chasing after Windows updates. Thanks for confirming that it works, and have an awesome weekend as well! 🙂
Windows Updates can run, but they can’t hide, from THE CHASER!! The Chaser always gets his update!
Hi,
I donated $5 – can I get a beta code for 7+ taskbar tweaker?
Thanks.
Hi Mark,
Thank you for the support, I appreciate it. I see that the code was emailed to you. Please let me if you didn’t receive it.
Virus detection in the latest beta v5.9.1.4:
https://www.virustotal.com/gui/file/1ddbd49ace7914bf2d297263b696fbf42662e41a768e50236455674044b5b01c/detection
Those are false positive detections. False positives are unfortunately common for new versions of 7+ Taskbar Tweaker and for beta versions which are less common. Please see the FAQ here and this blog post.
Hello RaMMichael.
I would like to let you know that I get the following error since I upgraded to
Windows 10 Insider Preview 20231:
7+ Taskbar Tweaker: Could not load library (5)
Hi Patrick,
Please try the newly released v5.9.1.5 beta.
Thank you very much for the quick update.
Works again as usual.
The only thing I had to-do was to disable the Real-Time detection from MS Defender because it falsely detected your setup as a Virus.
Greetings Michael!!
The Chase is back on! I’m running 7+ TT v5.9.1.4 Beta and got the following startup error after an update:
“7+ Taskbar Tweaker: Could not load library (5)”
I just upgraded to the following Windows Home Insider Preview build:
Windows 10 Home Insider Preview
Version 2004
Installed Oct 9, 2020
OS Build 20231.1000
The Chase is back on after only 8 days. Who’s running the circus at Microsoft…they need to clean up their act??
Good Luck with the Chase Mr. Chaser! We believe in you!!
The chase is back on indeed. Please try v5.9.1.5 beta.
And the chase is over! Nicely done and in record time sir! Have yourself a great weekend and thanks so much for taking care of this so quickly.
Hello RaMMichael!
Thank you for the fantastic 7tt software. It seems that the defender in Windows 10 19042.541 completely blocks 7tt from installing and running. The beta version installed in my notebook has been removed silently by the windows defender. I cannot even download a new beta version to install since each download is blocked and removed. How to solve this problem?
Hi,
If you don’t need the features of the beta version, it’s best to use the latest non-beta version since it has much less issues with false positive detections. If you need the beta version, you can try adding the tweaker’s setup file and installation folder to the exclusions list of your antivirus software. You can also contact your antivirus company about it, usually they remove the false positive detection after a couple of days.
5.9.15 is being detected in the latest insider build as a severe threat. I was able to install it, but I had to add a manual folder exclusion to even get it to run. Is there anything you can do?
Please see my comment just above yours (here).
My antivirus – Bitdefender suggested that this app has something to do with the HDD encryption ransomware attack. I had to uninstall it. Any idea why?
I run windows 10.
That’s probably a false positive detection. 7+ Taskbar Tweaker has nothing to do with encryption, and it surely isn’t a ransomware. False positives are unfortunately common for new versions of 7+ Taskbar Tweaker and for beta versions which are less common. Please see the FAQ here and this blog post.
hi, after the windows update relased today (kb4580386), im getting the library 107 error.
im using 5.9.1.5 beta
same here. i’m using Win 10 Version 1909 (Build 18363.1171).
After Windows Updates (KB4580386 and KB4580980), neither v5.9.1.5 nor v5.9.1 is working.
Please try the newly released v5.9.1.6 beta.
Had several warnings when installing the 5.9.1.5 beta, but it worked.
Interesting: At first I couldn’t even save the beta locally. But after opening Windows Defender and made it mark this beta as no thread, everything is fine.
Look in “Bedrohungsverlauf” <-[that’s German, don’t know what this might be in English versions] – Once fixed, no problems any more.
Thanks a lot for this tool. Just donated another 10 US$, because it’s just worth it.
Thank you for the support and for the Defender tip for other users.
Forgot to mention: Warnings came up after updating to Win10 Pro Version 20H2 (Build 19042.572) <- that’s what “winver” tells me right now.
Anyway: Defender warned me, I could download the beta, but I had to confirm. But file was automatically deleted after download. Until I checked the quarantine and restored file from there.
If I’m not mistaken, build 19042.572 is supported by the latest the non-beta version, 5.9.1, as well. Like the beta, it also shows a warning, but should work.
Yes, it did work. But I had some problems to tell my PC not to delete the installer while installing. Not that big of an issue, I think. But indeed, there were some hiccups for me at October 21th.
Please add more options for donate.
I can’t use paypal in my situation, so it would be nice if you add something like donationalerts.
Hi Viktor,
Thank you for considering a donation. Bitcoin, WebMoney are also possible. The Bitcoin wallet can be found in the donate page. For WebMoney, please email me.
Hi RaMMicHaeL, many thanks for your great software!
Is it possible to hide only one label, by window name for example?
I’m running Windows 7 x64.
Hi,
You can hide labels selectively according to the AppId. See the FAQ for a screenshot. If you want to affect a single item, you can change its AppId to a random one, but it will be temporary. There’s no option to set rules according to a window name or properties other than the AppId.
Hi,
I had searched in Taskbar Inspector, but obviously not enough.
Thank you, it works perfectly.
New Update for Windows 10 20H2 19042.608
7+ Beta works not with this 20H2 Version.
I’m on 10942.572 and couldn’t even save the installer file locally. But after looking in quarantine and restoring file from there, marking it as “no threat” – everything was fine.
So I think the beta should work on your PC, too. Defender doesn’t seem to like it. Some fiddeling surely needs to be done.
Please try the newly released v5.9.1.7 beta.
Oh man,
This app is awesome, but I really need an option “”Don’t group unpinned items”
or “Only group pinned items:”
– So the opposite of the option that is available now!
Scratch that. I’m an idiot.
Taskbar Inspector 🙂
I was wondering if the support codes are still available for the beta versions? I’ve donated in the past a couple of times, I can donate again if needed. I am on the Windows Preview channel so I understand why the last version of the beta may not be working now. I really love this taskbar tweaker. After downloading and installing the newest beta, the box or option for the code aren’t showing. I had uninstalled and reinstalled, but it didn’t show. Could this be because I chose to save my personal settings?
Any help is greatly appreciated. Thank you!!!
Hi Chris,
Yes, the codes work. It’s possible that the latest insider version is not supported, I need to check that. Unfortunately, the update pace is much higher lately, my priority now is to fix support for non-insider versions 1909 (broken with a recent update) and 20H2 (just released).
Regarding the code, you can check or remove it via registry, under:
HKEY_CURRENT_USER\SOFTWARE\7 Taskbar Tweakerv5.9.1.6 Beta does not work on Windows 10 version “19042.608”
Please try the newly released v5.9.1.7 beta.
v5.9.1.6 Beta does not work on Windows 10 version “19042.608”
Thanks you 🙂
Yes, v5.9.1.6 beta doesn’t, but v5.9.1.7 beta should 🙂
Yes new build fixed it 🙂
Unfortunately v5.9.1.6 doesn’t work on 19042.608 T.T
Please try the newly released v5.9.1.7 beta.
V5.9.1.7 beta works with Windows 10 19042.608 now, thanks so much, well done!
Strangely still downloaded as v5.9.1.6
Perhaps you have v5.9.1.6 cached, try downloading form an incognito window.
Now work fine, thank you.
Thank you so much for fixing the incompatibility caused by update KB4580386 of Windows 10 version 1909!
Have a great day!